Õppimises ja õpetamises osalevatele subjektidele esitatava info ontoloogia

Kuue mõõtmelise koordinaatteljestiku põhiidee

Inimestes, masinates ja nende vahelises ruumis tekkivates seostes edastatav materiaalne sisu on oma olemuselt keeruline. Keerulisus peegeldub ka sisulise tähendusega kirjelduste (ehk info) struktuuris. Tervikliku info struktuuris eristatakse küllaltki selgelt koostist (organization) ja teostust (realization) ning nendes mõlemas veel ülesehitust (architecture). Tegelike asjade koostisosasid ja nendevahelisi seoseid, milles toimub sisu liikumine (ehk sisuline voog), kirjeldatakse üheskoos ja visualiseeritakse topoloogia-skeemidega. Reaalsete ehk toimivate asjade (entity), mudelite ja süsteemsete teooriate kirjeldustes, on koostis ja teostus ning koostise ülesehitus ja teostuse ülesehitus põhimõtteliselt erinevad kuid siiski põimunud. Tehnilise hariduse andmisel õppuritele edastab ja esitab õppejõud infot teatud süsteemiga piiritletud materiaalsete koostisosade kirjeldamiseks. Teine osa õppuritele edastatavast infost esitab sisulist liikumist mis on (teostub) nende koostisosade sisemistes või vahelistes seostes. 

Üks oluline mõiste mis aitab meil kirjeldada teoreetiliste, modelleeritud ja reaalsete asjade koostist ja nende vahel toimuvaid sisulisi liikumisi on ruumi dimensioon (e. mõõde või ulatus). Leidub palju erinevaid kirjanduse allikaid mis selgitavad dimensiooni mõistet. Füüsikud on mänginud olulist osa dimensioonide paremas mõistmises ja meie kui subjektide arusaamise kujundamisel aegruumist ja materiaalsetest objektidest.

 Suhteliselt üldise dimensiooni sisulisemal modelleerimisel saadakse juba konkreetsed objektid ehk nn koordinaatteljed, mida subjektid saavad siis kasutada huvitava koostisosa ja selle liikumise erinevate omaduste (ka parameetrite) väärtuste mõõtmisel. Ühes punktis lõikuvatest joontest   koostatud ruumilist objekti ehk ruumi koordinaatteljestikku saab kasutada visuaalse võrdlusobjektina. Füüsilist (arv)teljestikku saab kasutada mõõtmistel etalonobjektina. [123].

René Descartes võttis kasutusele lõikuvatest ja üksteise suhtes ristuvatest sirgjoontest visuaalse objekti (x-, y- ja z- teljestiku), et modelleerida geomeetrilisi objekte geograafilises ruumis. Silmadega näeb inimene enda ümber geomeetrilisi objekte kolmemõõtmelises (geograafilises) ruumis.

Aastal 1843 võttis matemaatik William R. Hamilton kasutusele neljamõõtmelise aegruumi mudeli [124]. Fundamentaalne konstant c (valguse kiirus) võimaldab kasutajatel geomeetriseerida aega (ct) ja seega muuta seda dimensiooni visuaalsemaks. Diagrammidel visualiseeritakse ajalist kestust sirgjoonega, mille pikkus on määratud aja algus- ja lõppväärtusega. Geomeetriseerimine ei tähenda, et aja mõiste on geomeetriline. Aegruumi standardiseeritud raamistikku kasutatakse nüüdisajal mis tahes lihtsa või keerulise objekti sisu väärtuse tuvastamiseks ja määramiseks.

Toimivate asjade (objektide) liikumised (nende omadused) ei ole olemuselt geomeetrilised. Sisulise liikumise koostise ja teostumise mõistmisel tuleb meile abiks mitmedimensioonilise ruumi mõiste.

Teadlased on uue dimensiooni lisamist üldisesse relatiivsusteooriasse oodanud alates 1920 aastast kui Theodor Kaluza ja Oskar Klein soovitasid relatiivsusteooriat mis sisaldab viiendat dimensiooni. Nüüdisaegses teoorias on hästi teada ja üldiselt tunnustatud arusaam, et ruum on mitmemõõtmeline ja isegi elementaarosakesed ei ole lihtsalt punktid vaid võivad koosneda väga väikestest stringidest [125]. Hetkel on uurimise all Ruumi-Aja-Mateeria teooria oma ekstra viienda dimensiooniga, mis pakuti välja S. Wesson ja tema kolleegide poolt. Selle teooria kohaselt on kõik materiaalsed väljad viiendas dimensioonis ning võivad edastuda suuremamõõtmelises vaakumis [126], [127]. On üritatud siduda aegruumi ja tegelikult toimuvaid elektromagnetismi nähtusi kasutades viiendat dimensiooni [123], [128].

Meie meeltest saadud ruumilise info põhjal suudab aju visualiseerida geomeetriliste asjade koostist ja tajuda seoseid (topoloogiat), kuid ei saa määrata veel aja väärtust, vaadeldava liikumise kõigi erinevate omaduste väärtust (sisu kvantiteeti) ja nende omaduste väärtuslikkust (kvaliteeti).

Geograafilises ruumis avalduva geomeetrilise subjekti ja objekti ning nende koostisosi visualiseeritakse punktidega ja nende topoloogilisi seoseid punktide paaridena millele on lisatud konkreetsed koordinaadid, mis saadakse mõõtmisel milles kasutatakse koordinaattelgede süsteemi. Subjekti ja objekti (ehk ressursi) geograafiliste punktide vahelist topoloogilist seost kirjeldab Joonis 6.1 [56]. Topoloogiline seos koostatakse vähemalt kahest ühendusest.

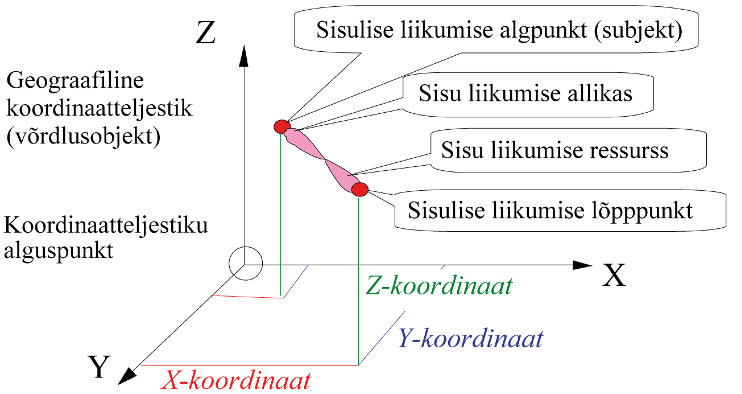
Joonis 6.1 Geograafilise telje grupp ja mõiste liikumise loogiline sisu [56].

Kasutades nägemismeelt ja oma ajataju lisab inimene geomeetrilisele ruumile veel ajamõõtme. Veelgi keerukamate ,valdavalt vaid matemaatiliselt kirjeldatud, viie ja enama mõõtmeliste süsteemide visualiseerimine on koolitamata õppurile üsana raske.

Nüüdisaja hariduse lahendamata probleem seisneb puudulikult mõtestatud visualiseerimises, mistõttu tehnilisi projekteerijaid õpetatakse kasutama peamiselt nelja tuntud põhidimensiooni nii subjektide kui objektide koostise kui sisulise liikumise mõõtmisel, kirjeldamisel või sünteesimisel. Samuti kasutatakse nelja põhidimensiooni ka asjadevahelistes seostes toimuva liikumise kvaliteedi kirjeldamisel. Sellise meetodi põhjal tekivad sageli pikad ja kohmakad kirjeldused.

Öeldakse, et üks hea pilt asjast suudab edastada rohkem infot liikumise kohta kui tuhat sõna. Inimene tunnetab maailma koostist vormides kirjeldustesse pilte ja oma ajus kolmemõõtmelisi geomeetrilisi kujutisi. Geomeetrilise süsteemi, teooria, mudeli, subjekti, objekti ja nende eri osade (näit. punktide) vahelisi topoloogilisi seoseid kirjeldatakse koolides juba mitu sajandit tuntud x,y,z telgede abil.

Punktidevahelisi seoseid ja nendes toimuvat liikumist visualiseeritakse joonte ja nooltega mis mõningal määral selgitab liikumise olemust. Selline kolmedimensiooniline (geomeetriline) kujutis annab edasi asja liikumise olemust, kuid mitte eriti täpselt. Jooned esitavad liikumist mis jääb tegelikkuses väljapoole geograafilist ruumi. Asja sisu liigub ruumis hajusamalt ja keerukamalt kui seda punktid ja jooned suudavad silmadele esitada. Toimuva liikumise sisu muundust, (sisu kvaliteedi muutust) selgitatakse õppematerjalides tavaliselt eraldi matemaatiliste sümbolite ja valemitega.

Seoses infotehnoloogia võimaluste kasvuga ja kasutuse laienemisega hariduse andmisel ning edastatava info mahtude ja keerukuse tohutu suurenemisega on vaja olemasoleva info mõistmiseks paremaid struktureerimise meetodeid ja vahendeid. Uued struktureerimise meetodid peaksid võimaldama geomeetriseerida ka ajalise liikumise sisu väärtusi ja keerukalt hajutatud (põimuvaid) sisulisi muundumisi. Uued tarkvaravahendid peaksid aitama teha liikumist kirjeldustes subjektile visuaalseks.

Süsteemis, teoorias, mudelis, objektis, subjektis ja nendevahelistes seostes teostuva liikumise kogu keerukust, mida õppuri meeled ja koolitamata aju ei suuda tavaliselt haarata, võiks kirjeldada täiesti uute teostuse dimensioonide põhjal moodustatud koordinaatteljestikuga. Uus visuaalselt ristuvatest joontest moodustatud teostumistelgede kolmik on esitatud Joonis 6.2.

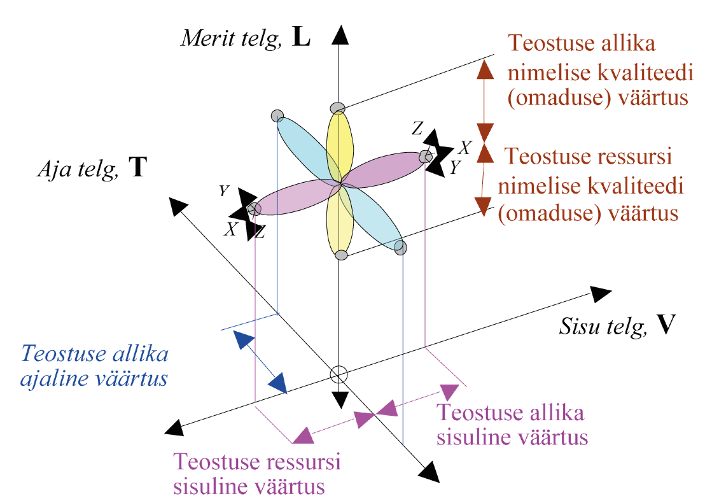
Joonis 6.2 Teostustelgede grupp [56]

Haridusalal praktiliselt puudub laialt tunnustatud koolituse või tehnilise inseneriteaduse ja insenerihariduse metoodika, mis põhineb näiteks kuuel põhimõõtmel. 

Geomeetrilise Objekti sisulised omadused avalduvad geograafilistes punktides. Kahte punkti ühendavas seoses toimuva liikumise (sisuliste omaduste kvantiteedi) kirjeldamiseks orienteeritakse uue teostusteljestiku sisu (edastuse) telg nii, et see läbiks vaadeldava seose alguspunkti ja lõpppunkti. Kujutagem nüüd, et meile kõigile tuntud geograafiline ruum on uue teostusruumi alamruum. Kuuedimensioonilist ruumimudelit (6D) valdav ja kasutav õppur saab kujutada (geomeetriseerida, visualiseerida) lisaks erinevatele geograafilistele (geomeetrilistele) punktidele ka teostuse aega, liikumise erinevate omaduste kvantiteeti ja nende omaduste erinevaid kvaliteete. Seega suudab ta raskusteta mõelda kuuedimensiooniliselt. Kuuemõõtmelise liikumise visuaalne kirjeldus on esitatud Joonis 6.3.

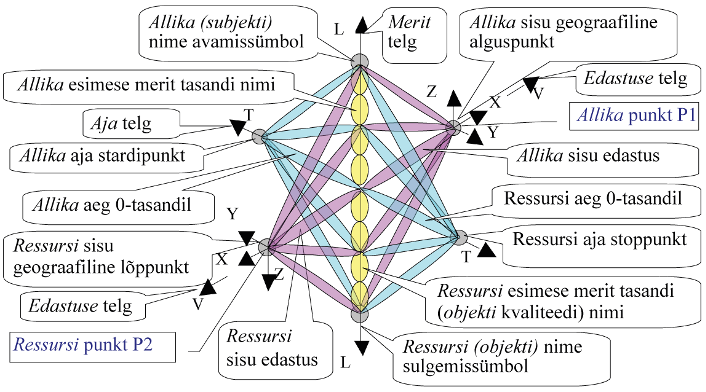
Joonis 6.3 Keerulise sisulise liikumise visuaalne kirjeldus 6D-ruumis [56]

Tõenäoliselt me juba kasutame kuuedimensioonilist ruumimudelit kirjeldamaks keeruliste objektide koostist ja teostust iga päev, kuid me ei märka seda, ega pööra sellele tähelepanu kuna meid pole õpetatud ruumi nägema kuuedimensiooniliselt?

Hariduse valdkonnas on materiaalsete üksuste koostise ja realiseerumise (teostumise) efektiivseks kirjeldamiseks vajalik üldisem selgitusmeetod. Uus kuuedimensiooniline ruum ja vastav visualiseerimismeetod võimaldab kasutada infoajastul loodud andmete modelleerimise võimalusi ja vahendeid [56]. Kuuedimensioonilise ruumi teooria on ontoloogia, sest põhineb tegeliku elu subjektide ja objektide liikumiste vaatlustel, mõõtmisel ja kirjalikult salvestatud faktidel.

Kvalifikatsioonisüsteemis (mille piires toimivad haridus- ja kutsesüsteem), ja tööturul tegutsevate ettevõtjate, töötajate ja nende töövahendite ning haridust omandavate õppurite ja nende tehniliste objektide vahelise sisulise liikumise visuaalsel kirjeldamiseks on doktoritöös kasutusele võetud eelnimetatud kuuedimensiooniline ruumimudel ja selles uudsena esitatud teostuse ontoloogia. Selle abil saab visualiseerida mitte ainult geograafilisi asju, vaid samas ka geomeetriseerida asjades ja nende vahelistes seostes toimivat liikumist, selle aega, sisu omaduste edastuse väärtusi ja liikumise ülesehituses omaduste väärtuslikkust. Kuna liikuva sisu (omaduste) väärtuslikkust ehk kvaliteeti esitatakse tajumiseks ja ka visualiseeritakse sõnadega, siis erineb uus merit telg tavapärasest arvteljest sellega, et jaotised ei ole tähistatud arvudega vaid nimetustega.

Kuuemõõtmelise ruumimudeli lühikirjeldus ja selle kasutamisvõimaluste selgitus visuaalsete õppematerjalide loomisel on esitatud järgnevates punktides.